| (23 révisions intermédiaires par le même utilisateur non affichées) | |||
| Ligne 13 : | Ligne 13 : | ||
La gravitation est une interaction physique responsable de l’attraction des corps avec une masse. | La gravitation est une interaction physique responsable de l’attraction des corps avec une masse. | ||
| − | Le but de l’atelier est de comprendre comment fonctionne la gravitation par des expériences. | + | Le but de l’atelier est de comprendre comment fonctionne la gravitation par des expériences visuelles qui simulent notre système solaire. |
}} | }} | ||
{{Materials}} | {{Materials}} | ||
| Ligne 22 : | Ligne 22 : | ||
* Un draps (ou toile souple) | * Un draps (ou toile souple) | ||
* Des balles de poids différents (boule de pétanque, balle de tennis, balle de ping-pong, billes...) | * Des balles de poids différents (boule de pétanque, balle de tennis, balle de ping-pong, billes...) | ||
| + | |||
}} | }} | ||
{{Tuto Step | {{Tuto Step | ||
|Step_Title=Tendre un draps à l’horizontal | |Step_Title=Tendre un draps à l’horizontal | ||
|Step_Content=Tendre un drap à l’horizontal à l’aide des participants ou de supports (chaises par exemple) . Ce drap représente l’espace-temps. | |Step_Content=Tendre un drap à l’horizontal à l’aide des participants ou de supports (chaises par exemple) . Ce drap représente l’espace-temps. | ||
| + | L'espace-temps est une représentation mathématique de l'espace et du temps comme deux notions inséparables et s'influençant l'une l'autre. Cette idée d’un espace-temps déformé par la masse provient de la théorie de la relativité générale d’Albert Einstein (1915). | ||
| + | |||
| + | [[Fichier:Espace-temps.png|500px]] | ||
| + | |||
| + | ⚠️ Attention : le drap est une représentation simplifiée. | ||
| + | En réalité, l’espace est déformé dans toutes les directions, pas seulement vers le bas, et il n’y a pas de gravité « extérieure » qui tire les objets vers le centre du drap. | ||
| + | |||
}} | }} | ||
{{Tuto Step | {{Tuto Step | ||
| − | |Step_Title= | + | |Step_Title=Placez une boule de pétanque au centre |
| − | |Step_Content= | + | |Step_Content=Demandez à une personne de placer une boule de pétanque (ou un autre objet lourd) au centre du draps. Cette boule représente ici le Soleil. Le Soleil est une étoile située au centre du système solaire : une énorme boule de gaz (surtout hydrogène et hélium) âgée d’environ 4,6 milliards d’années, dont l’énergie provient de la fusion nucléaire et rend possible la vie sur Terre en fournissant lumière et chaleur. Le Soleil représente à lui seul environ 99,854 % de la masse du système solaire, Jupiter représentant plus des deux tiers du reste. |
| + | |||
| + | [[Fichier:Boule petanque.png|200px]] | ||
| + | [[Fichier:Soleil.jpg|200px]] | ||
| + | |||
| + | Que remarque-t-on ? | ||
| + | |||
| + | ................................................................................................................................................ | ||
| + | |||
| + | Réponse : « On remarque que la boule de pétanque déforme ("creuse") le draps. Autrement dit, le Soleil déforme l'espace-temps proche de lui » | ||
| + | |||
}} | }} | ||
{{Tuto Step | {{Tuto Step | ||
|Step_Title=Le principe de la gravitation | |Step_Title=Le principe de la gravitation | ||
| − | |Step_Content= | + | |Step_Content=Lancez sur le draps une balle de tennis et observer se qu’il se passe. |
| − | Cette balle représente ici une planète. | + | Cette balle représente ici une planète. Dans le système solaire on trouve huit planètes avec plus de deux-cents lunes, les cinq planètes naines et leurs neuf satellites connus, ainsi que des milliards de petits corps (les astéroïdes, les comètes, les poussières cosmiques, etc.). |
| + | |||
| + | [[Fichier:Balle_tennis.jpg|200px]] | ||
| + | [[Fichier:Planete.jpg|200px]] | ||
Que remarque-t-on ? | Que remarque-t-on ? | ||
| Ligne 41 : | Ligne 62 : | ||
................................................................................................................................................ | ................................................................................................................................................ | ||
| − | Réponse : « | + | Réponse : « La balle suit les déformations du drap et se rapproche de la boule de pétanque. |
| + | La planète suit la géométrie de l’espace-temps déformé par le Soleil, ce qui se manifeste comme une attraction gravitationnelle. » | ||
}} | }} | ||
{{Tuto Step | {{Tuto Step | ||
|Step_Title=Les différents paramètres | |Step_Title=Les différents paramètres | ||
| − | |Step_Content=Nous allons étudier comment est | + | |Step_Content=Nous allons étudier comment est modifiée la trajectoire de la balle de tennis en fonction de ses différents paramètres physique : |
| + | * La masse | ||
* La direction initiale | * La direction initiale | ||
* La vitesse initiale | * La vitesse initiale | ||
| − | * La masse | + | * La distance initiale au Soleil |
| + | |||
| + | }} | ||
| + | {{Tuto Step | ||
| + | |Step_Title=La masse | ||
| + | |Step_Content=Lancez à plusieurs reprises des objets de masses différentes à chaque fois : | ||
| + | |||
| + | *une bille (une masse légère) représentant un astéroïde, | ||
| + | *une balle de tennis (une masse modérée) représentant une planète, | ||
| + | *une autre boule de pétanque (une masse lourde) représentant une autre étoile comme le Soleil | ||
| + | |||
| + | Voici les ordres de grandeur des masses (en kilogrammes), du plus massif au plus petit : | ||
| + | *Soleil : ~ 10³⁰ kg | ||
| + | *Planètes : | ||
| + | **planètes géantes (Jupiter, Saturne…) : ~ 10²⁶ à 10²⁷ kg | ||
| + | **planètes telluriques (Terre, Mars…) : ~ 10²³ à 10²⁴ kg | ||
| + | *Astéroïdes : | ||
| + | **gros astéroïdes (comme Cérès) : ~ 10²⁰ à 10²¹ kg | ||
| + | **petits astéroïdes : ~ 10⁹ à 10¹⁵ kg | ||
| + | |||
| + | Que remarque-t-on ? | ||
| + | |||
| + | ................................................................................................................................................ | ||
| + | |||
| + | Réponse : « | ||
| + | *La bille déforme très peu le drap et est fortement attirée par la boule de pétanque. | ||
| + | |||
| + | *La balle de tennis déforme modérément le drap. | ||
| + | |||
| + | *Les deux boules de pétanque se déforment mutuellement et s’attirent. | ||
| + | |||
| + | |||
| + | |||
| + | Conclusion : En réalité, dans un même champ gravitationnel, tous les objets chutent de la même façon. | ||
| + | Ce n’est pas la masse de l’objet qui modifie sa trajectoire, mais la déformation de l’espace-temps qu’il crée lui-même.» | ||
}} | }} | ||
{{Tuto Step | {{Tuto Step | ||
|Step_Title=La direction initiale | |Step_Title=La direction initiale | ||
| − | |Step_Content= | + | |Step_Content=Lancez à plusieurs reprises la balle de tennis avec une direction différente à chaque fois : |
| − | *vers la boule de pétanque | + | *vers la boule de pétanque, |
| − | *vers l’extérieur du draps | + | *vers l’extérieur du draps et |
| − | *dans la direction perpendiculaire | + | *dans la direction perpendiculaire au centre. |
Que remarque-t-on ? | Que remarque-t-on ? | ||
| Ligne 63 : | Ligne 120 : | ||
................................................................................................................................................ | ................................................................................................................................................ | ||
| − | Réponse : « La direction initiale | + | Réponse : « La direction initiale détermine la forme de la trajectoire : chute directe, trajectoire elliptique ou orbitale (circulaire dans un cas particulier).» |
}} | }} | ||
{{Tuto Step | {{Tuto Step | ||
|Step_Title=La vitesse initiale | |Step_Title=La vitesse initiale | ||
| − | |Step_Content= | + | |Step_Content=Lancez à plusieurs reprises la balle de tennis avec une vitesse différente à chaque fois : |
*vitesse lente, | *vitesse lente, | ||
*vitesse modérée et | *vitesse modérée et | ||
*vitesse rapide | *vitesse rapide | ||
| + | |||
| + | Voici les ordres de grandeur des vitesses en km/h : | ||
| + | *Planètes autour du Soleil : ~ 10⁵ km/h (ex. Terre ≈ 1,1 × 10⁵ km/h) | ||
| + | *Astéroïdes : ~ 10⁵ km/h (même ordre de grandeur que les planètes) | ||
| + | *Soleil (autour du centre de la Voie lactée) : ~ 10⁶ km/h (≈ 7 × 10⁵ km/h) | ||
Que remarque-t-on ? | Que remarque-t-on ? | ||
| Ligne 77 : | Ligne 139 : | ||
................................................................................................................................................ | ................................................................................................................................................ | ||
| − | Réponse : « La vitesse initiale | + | Réponse : « La vitesse initiale influence la taille de l’orbite et le nombre de révolutions autour du Soleil.» |
}} | }} | ||
{{Tuto Step | {{Tuto Step | ||
| − | |Step_Title=La | + | |Step_Title=La distance initiale |
| − | |Step_Content= | + | |Step_Content=Lancez à plusieurs reprises la balle de tennis avec une distance initiale de la boule de pétanque différente à chaque fois : |
| + | |||
| + | *petite distance, | ||
| + | *modérée distance et | ||
| + | *grande distance | ||
| − | * | + | Voici les ordres de grandeur des distances au Soleil (en kilomètres) : |
| − | * | + | *Planètes : ~ 10⁸ à 10⁹ km (ex. Terre ≈ 1,5 × 10⁸ km) |
| − | * | + | *Astéroïdes (ceinture principale) : ~ 10⁸ km(entre Mars et Jupiter) |
| + | *Objets très lointains (au-delà de Neptune, Kuiper…) : ~ 10¹⁰ km | ||
Que remarque-t-on ? | Que remarque-t-on ? | ||
| Ligne 91 : | Ligne 158 : | ||
................................................................................................................................................ | ................................................................................................................................................ | ||
| − | Réponse : « La | + | Réponse : « Plus la distance initiale au Soleil est grande, plus l’orbite est large et plus la période de révolution est longue. » |
| + | |||
| + | [[Fichier:Distance_revolution.png|600px]] | ||
| + | |||
| + | }} | ||
| + | |||
| + | {{Tuto Step | ||
| + | |Step_Title=Conclusion | ||
| + | |Step_Content= | ||
| + | Cet atelier permet de visualiser la gravitation comme une conséquence directe de la déformation de l’espace-temps par la masse, conformément à la relativité générale d’Einstein. | ||
| + | |||
| + | Grâce à l’analogie du drap : | ||
| + | |||
| + | Le Soleil, très massif, déforme fortement l’espace-temps, ce qui influence le mouvement des planètes. | ||
| + | |||
| + | Les planètes ne sont pas « attirées » au sens classique, mais suivent les trajectoires naturelles imposées par cette déformation. | ||
| + | |||
| + | La trajectoire d’un objet dépend : | ||
| + | |||
| + | *de sa vitesse initiale, | ||
| + | |||
| + | *de sa direction initiale, | ||
| + | |||
| + | *de sa distance au Soleil. | ||
| + | |||
| + | Contrairement à une idée répandue, la masse de l’objet n’influence pas sa chute dans un même champ gravitationnel : tous les objets se déplacent de la même manière s’ils n’interagissent pas autrement. | ||
| + | |||
| + | Enfin, l’atelier montre pourquoi : | ||
| + | |||
| + | les planètes proches du Soleil ont des orbites courtes et rapides, | ||
| + | |||
| + | les planètes lointaines ont des orbites larges et des périodes très longues. | ||
| + | |||
| + | Cette expérience met en évidence que la gravitation n’est pas seulement une force invisible, mais l’expression de la géométrie même de l’Univers. | ||
}} | }} | ||
| − | |||
{{Notes}} | {{Notes}} | ||
{{Tuto Status | {{Tuto Status | ||
|Complete=Draft | |Complete=Draft | ||
}} | }} | ||
Version actuelle datée du 27 janvier 2026 à 10:08
Sommaire
- 1 Introduction
- 2 Atelier – La Gravitation visualisée
- 2.1 Étape 1 - Rassembler le matériel
- 2.2 Étape 2 - Tendre un draps à l’horizontal
- 2.3 Étape 3 - Placez une boule de pétanque au centre
- 2.4 Étape 4 - Le principe de la gravitation
- 2.5 Étape 5 - Les différents paramètres
- 2.6 Étape 6 - La masse
- 2.7 Étape 7 - La direction initiale
- 2.8 Étape 8 - La vitesse initiale
- 2.9 Étape 9 - La distance initiale
- 2.10 Étape 10 - Conclusion
- 2.11 Commentaires
Introduction
Atelier – La Gravitation visualisée
La gravitation est une interaction physique responsable de l’attraction des corps avec une masse.
Le but de l’atelier est de comprendre comment fonctionne la gravitation par des expériences visuelles qui simulent notre système solaire.Étape 1 - Rassembler le matériel
Matériel :
- Un draps (ou toile souple)
- Des balles de poids différents (boule de pétanque, balle de tennis, balle de ping-pong, billes...)
Étape 2 - Tendre un draps à l’horizontal
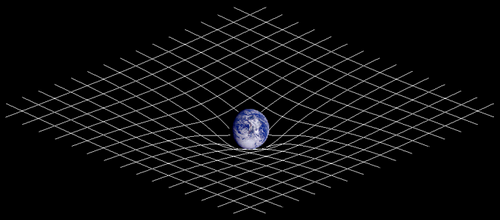
Tendre un drap à l’horizontal à l’aide des participants ou de supports (chaises par exemple) . Ce drap représente l’espace-temps. L'espace-temps est une représentation mathématique de l'espace et du temps comme deux notions inséparables et s'influençant l'une l'autre. Cette idée d’un espace-temps déformé par la masse provient de la théorie de la relativité générale d’Albert Einstein (1915).
⚠️ Attention : le drap est une représentation simplifiée. En réalité, l’espace est déformé dans toutes les directions, pas seulement vers le bas, et il n’y a pas de gravité « extérieure » qui tire les objets vers le centre du drap.
Étape 3 - Placez une boule de pétanque au centre
Demandez à une personne de placer une boule de pétanque (ou un autre objet lourd) au centre du draps. Cette boule représente ici le Soleil. Le Soleil est une étoile située au centre du système solaire : une énorme boule de gaz (surtout hydrogène et hélium) âgée d’environ 4,6 milliards d’années, dont l’énergie provient de la fusion nucléaire et rend possible la vie sur Terre en fournissant lumière et chaleur. Le Soleil représente à lui seul environ 99,854 % de la masse du système solaire, Jupiter représentant plus des deux tiers du reste.
Que remarque-t-on ?
................................................................................................................................................
Réponse : « On remarque que la boule de pétanque déforme ("creuse") le draps. Autrement dit, le Soleil déforme l'espace-temps proche de lui »
Étape 4 - Le principe de la gravitation
Lancez sur le draps une balle de tennis et observer se qu’il se passe.
Cette balle représente ici une planète. Dans le système solaire on trouve huit planètes avec plus de deux-cents lunes, les cinq planètes naines et leurs neuf satellites connus, ainsi que des milliards de petits corps (les astéroïdes, les comètes, les poussières cosmiques, etc.).
Que remarque-t-on ?
................................................................................................................................................
Réponse : « La balle suit les déformations du drap et se rapproche de la boule de pétanque. La planète suit la géométrie de l’espace-temps déformé par le Soleil, ce qui se manifeste comme une attraction gravitationnelle. »
Étape 5 - Les différents paramètres
Nous allons étudier comment est modifiée la trajectoire de la balle de tennis en fonction de ses différents paramètres physique :
- La masse
- La direction initiale
- La vitesse initiale
- La distance initiale au Soleil
Étape 6 - La masse
Lancez à plusieurs reprises des objets de masses différentes à chaque fois :
- une bille (une masse légère) représentant un astéroïde,
- une balle de tennis (une masse modérée) représentant une planète,
- une autre boule de pétanque (une masse lourde) représentant une autre étoile comme le Soleil
Voici les ordres de grandeur des masses (en kilogrammes), du plus massif au plus petit :
- Soleil : ~ 10³⁰ kg
- Planètes :
- planètes géantes (Jupiter, Saturne…) : ~ 10²⁶ à 10²⁷ kg
- planètes telluriques (Terre, Mars…) : ~ 10²³ à 10²⁴ kg
- Astéroïdes :
- gros astéroïdes (comme Cérès) : ~ 10²⁰ à 10²¹ kg
- petits astéroïdes : ~ 10⁹ à 10¹⁵ kg
Que remarque-t-on ?
................................................................................................................................................
Réponse : «
- La bille déforme très peu le drap et est fortement attirée par la boule de pétanque.
- La balle de tennis déforme modérément le drap.
- Les deux boules de pétanque se déforment mutuellement et s’attirent.
Conclusion : En réalité, dans un même champ gravitationnel, tous les objets chutent de la même façon. Ce n’est pas la masse de l’objet qui modifie sa trajectoire, mais la déformation de l’espace-temps qu’il crée lui-même.»
Étape 7 - La direction initiale
Lancez à plusieurs reprises la balle de tennis avec une direction différente à chaque fois :
- vers la boule de pétanque,
- vers l’extérieur du draps et
- dans la direction perpendiculaire au centre.
Que remarque-t-on ?
................................................................................................................................................
Réponse : « La direction initiale détermine la forme de la trajectoire : chute directe, trajectoire elliptique ou orbitale (circulaire dans un cas particulier).»
Étape 8 - La vitesse initiale
Lancez à plusieurs reprises la balle de tennis avec une vitesse différente à chaque fois :
- vitesse lente,
- vitesse modérée et
- vitesse rapide
Voici les ordres de grandeur des vitesses en km/h :
- Planètes autour du Soleil : ~ 10⁵ km/h (ex. Terre ≈ 1,1 × 10⁵ km/h)
- Astéroïdes : ~ 10⁵ km/h (même ordre de grandeur que les planètes)
- Soleil (autour du centre de la Voie lactée) : ~ 10⁶ km/h (≈ 7 × 10⁵ km/h)
Que remarque-t-on ?
................................................................................................................................................
Réponse : « La vitesse initiale influence la taille de l’orbite et le nombre de révolutions autour du Soleil.»
Étape 9 - La distance initiale
Lancez à plusieurs reprises la balle de tennis avec une distance initiale de la boule de pétanque différente à chaque fois :
- petite distance,
- modérée distance et
- grande distance
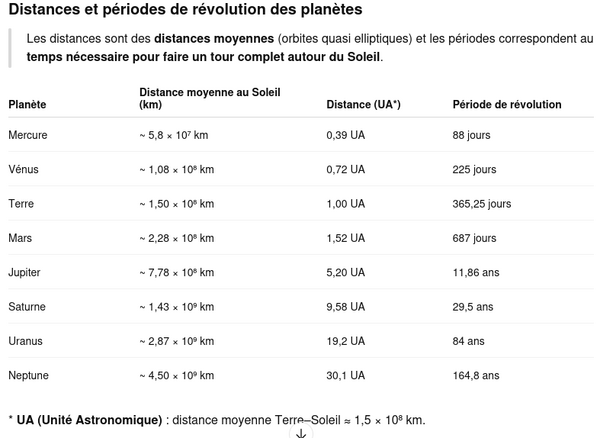
Voici les ordres de grandeur des distances au Soleil (en kilomètres) :
- Planètes : ~ 10⁸ à 10⁹ km (ex. Terre ≈ 1,5 × 10⁸ km)
- Astéroïdes (ceinture principale) : ~ 10⁸ km(entre Mars et Jupiter)
- Objets très lointains (au-delà de Neptune, Kuiper…) : ~ 10¹⁰ km
Que remarque-t-on ?
................................................................................................................................................
Réponse : « Plus la distance initiale au Soleil est grande, plus l’orbite est large et plus la période de révolution est longue. »
Étape 10 - Conclusion
Cet atelier permet de visualiser la gravitation comme une conséquence directe de la déformation de l’espace-temps par la masse, conformément à la relativité générale d’Einstein.
Grâce à l’analogie du drap :
Le Soleil, très massif, déforme fortement l’espace-temps, ce qui influence le mouvement des planètes.
Les planètes ne sont pas « attirées » au sens classique, mais suivent les trajectoires naturelles imposées par cette déformation.
La trajectoire d’un objet dépend :
- de sa vitesse initiale,
- de sa direction initiale,
- de sa distance au Soleil.
Contrairement à une idée répandue, la masse de l’objet n’influence pas sa chute dans un même champ gravitationnel : tous les objets se déplacent de la même manière s’ils n’interagissent pas autrement.
Enfin, l’atelier montre pourquoi :
les planètes proches du Soleil ont des orbites courtes et rapides,
les planètes lointaines ont des orbites larges et des périodes très longues.
Cette expérience met en évidence que la gravitation n’est pas seulement une force invisible, mais l’expression de la géométrie même de l’Univers.
Dernière modification 27/01/2026 par user:ZAB.
Draft